Playing with numbers

Its fun to play with numbers!

I generated all the kaprekar series for 2-digit to 50-digit numbers and tried to look for "patterns". Found some interesting behavior for the number of series found. Here are my observations.

Number of Series

It may not come as a surprise that the number of Kaprekar series increase with the number of digits in the numbers that you are dealing with. For e.g., all 4-digit number lead to only one series (excluding the degenerate case of 0) - 6174 - of size 1; while 5-digit numbers could end up in one of three series one of size 2 and two of size 4.

If the total number of series for a given number of digits is plotted against the number of digits we get an interesting graph -

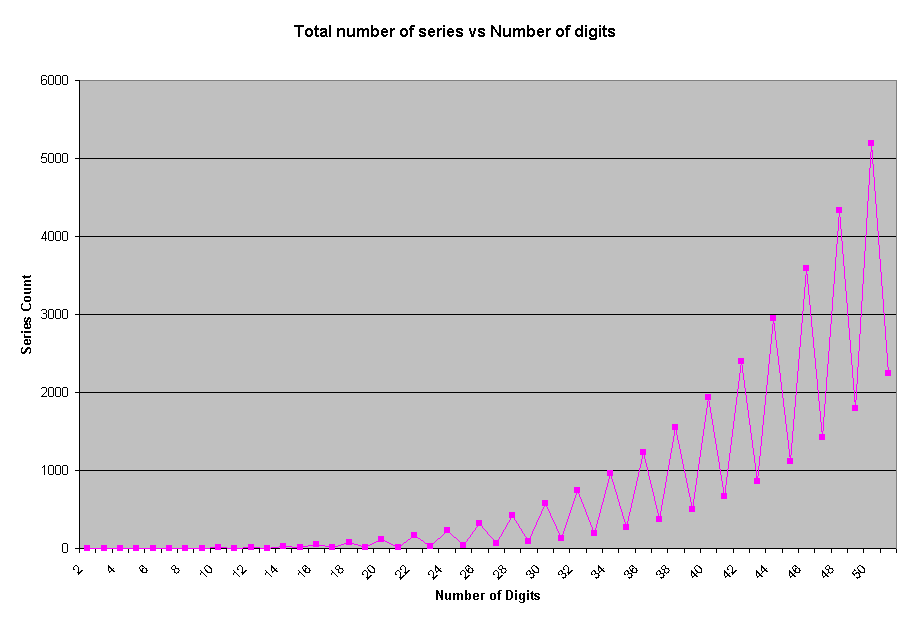
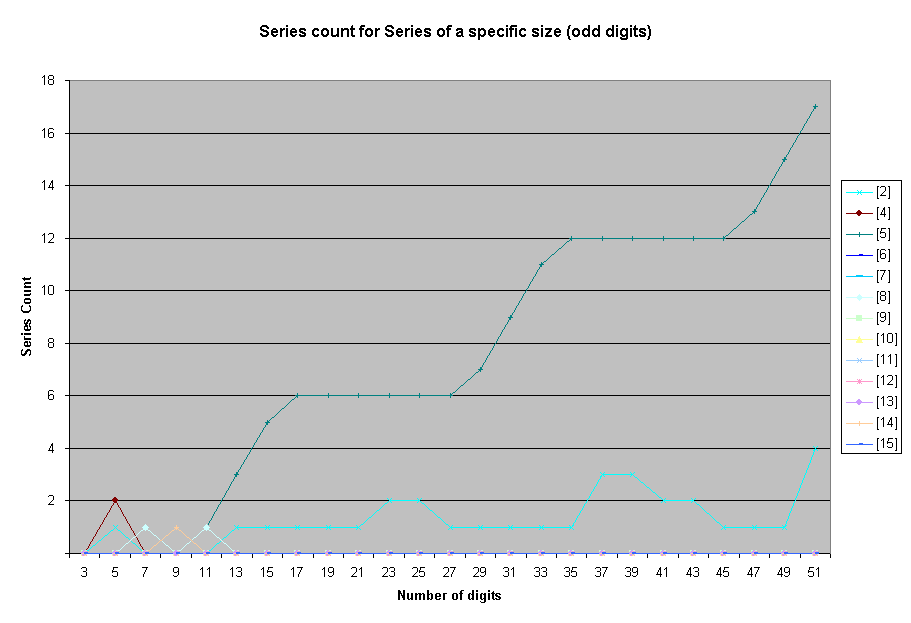
At first glance this graph looks pretty random. But look again. Split the graph into two graphs -

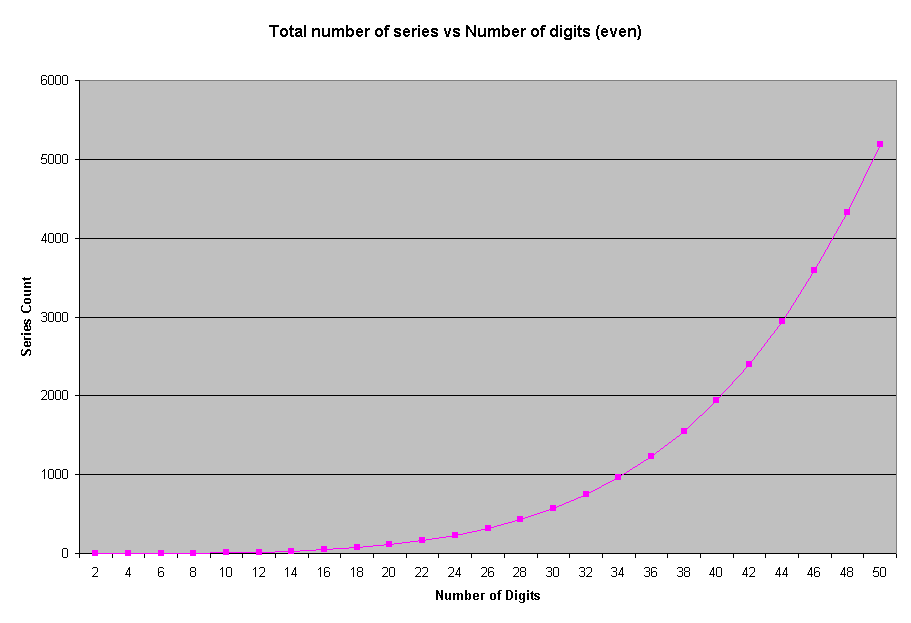
The number of kaprekar series against the number of digits - for even digits

The number of kaprekar series against the number of digits - for odd digits

The total number of series increases steeply with the number of digits. Whats interesting is that the total number for even number of digits is way higher than the total number for odd number of digits.

Series Size

Its interesting to observe the series size as the number of digits increases.

Until 8-digit numbers there are no series of size 3. For numbers with more than 22-digits, the majority of the series are of size 3! In fact, the number of series of size other than 3 is insignificant.

series count against number of digits for various series size.

After series of size 3, single number series are most prevalent followed by series of size 5.

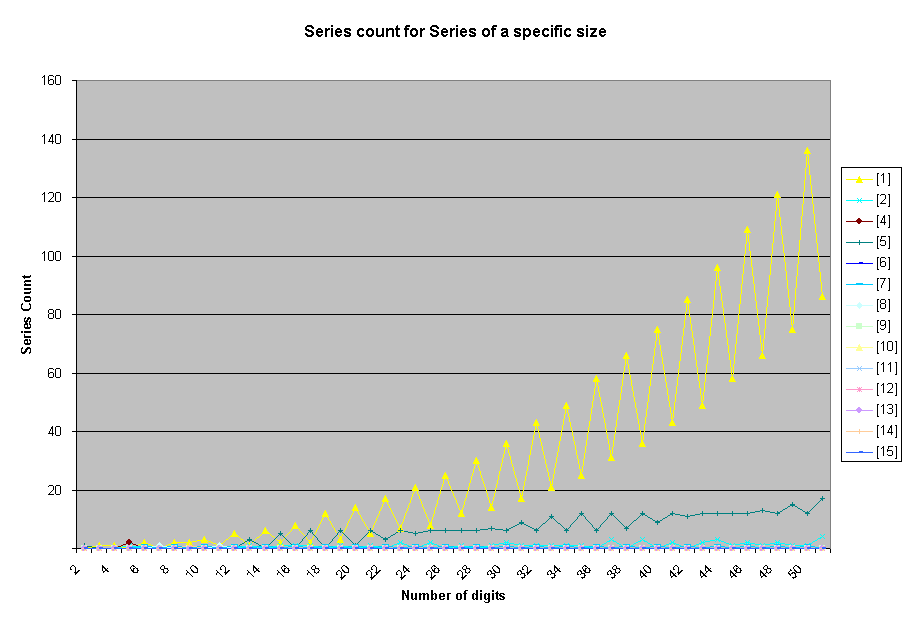
series count against number of digits for various series size (Other than 3).

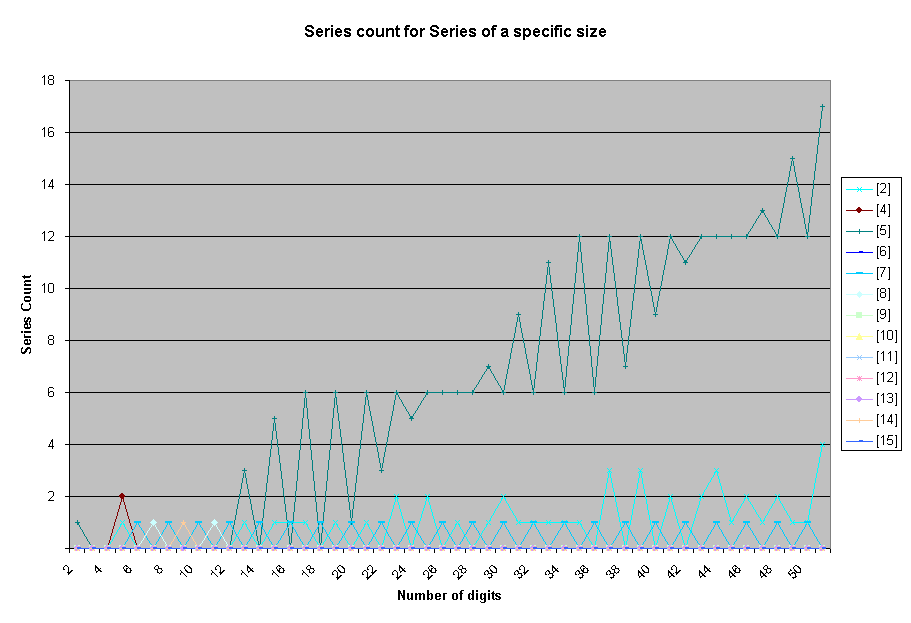
series count against number of digits for various series size (other than 1 and 3).

The pattern of growth for series of size 3 and 1 is similar to the one observed for the total number of series. The growth pattern for series for size 5 is different. We can again split the graph for even and odd number of digits to see the pattern.

series count against number of digits (only even digits) for various series size (other than 1 and 3)

series count against number of digits (only odd digits) for various series size (other than 1 and 3)

Size 4 series

I found only 2 series of size four and both of them are for 5-digit numbers!


74943 -> 62964 -> 71973 -> 83952 -> repeat

63954 -> 61974 -> 82962 -> 75933 -> repeat

Size 6 series

There are no size 6 series! Also there are no series of sizes 9 to 13.

Size 7 series

The first series of size seven is for 6-digit numbers. And for each even digit number after 6 there is one and only one series of size 7!

Size 8 series

There are only two series of size 8 - one for 7 and another for 11-digit numbers.



87331976622 -> 86542965432 -> 76320987633 -> 96442965531 ->
87320987622 -> 96653954331 -> 86330986632 -> 96532966431 -> repeat



8429652 -> 7619733 -> 8439552 -> 7509843 -> 9529641 -> 8719722 ->
8649432 -> 7519743 -> repeat

Longest Series

The longest series is a size 14 series for 9-digit numbers.


865296432 -> 763197633 -> 844296552 -> 762098733 -> 964395531 -> 863098632 -> 965296431 ->
873197622 -> 865395432 -> 753098643 -> 954197541 -> 883098612 -> 976494321 -> 874197522 -> repeat

Digits ending in a single series

There are only 4 digits that end in a single series - 2, 3, 4 and 7. Of these, 3 and 4 digit numbers end up in a single number - 495 and 6174 respectively. While 2 and 7 digit numbers end in a series of size 5 and 8 respectively.


9  -> 81 -> 63 -> 27 -> 45 -> repeat


8429652 -> 7619733 -> 8439552 -> 7509843 -> 9529641 -> 8719722 ->
8649432 -> 7519743 -> repeat

Note

The above statements were made based on the series generated for 2 to 50-digit numbers. They may change based on series generated for larger numbers.